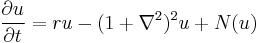Swift–Hohenberg equation

The Swift–Hohenberg equation (named after Jack B. Swift and Pierre Hohenberg) is a partial differential equation noted for its pattern-forming behaviour. It takes the form

\frac{\partial u}{\partial t} = r u - (1%2B\nabla^2)^2u %2B N(u)

where u = u(x, t) or u = u(x, y, t) is a scalar function defined on the line or the plane, r is a real bifurcation parameter, and N(u) is some smooth nonlinearity.

The equation is named after the authors of the paper[1], where it was derived from the equations for thermal convection.

The webpage of Michael Cross[2] contains some numerical integrators which demonstrate the behaviour of several Swift–Hohenberg-like systems.

Applications

Geometric Measure Theory

The equation has been used for finding a solution to the Kelvin Problem on minimal surfaces.

References

  1. ^ J. Swift and P.C. Hohenberg, Hydrodynamic fluctuations at the convective instability, Phys. Rev. A 15, 319–328 (1977)
  2. ^ Java applet demonstrations